미분적분학의 체계는 17세기에 영국의 수학자 뉴턴(Newton, I.; 1642∼1727)과 독일의 수학자 라이프니츠(Leibniz, G. W.; 1646∼1716)에 의하여 거의 같은 시대에 독립적으로 세워졌다. 그 후 많은 수학자들에 의하여 연구와 발전이 진행되었으며, 코시(Cauchy, A. L.; 1789∼1857)를 거쳐서 현재와 같은 미분적분학의 형태가 가추어졌다.

  실은, 뉴턴 이전에 이미 미분에 관한 선행적인 연구가 싹트고 있었다. 페르마(Fermat, P.; 1601∼1665)는 다항함수 y=f(x)가 나타내는 극대점과 극소점을 찾아 낼 수 있는 대단히 교묘한 방법을 고안하였다. 극대점과 극소점에서는 접선이 수평이 되어야 한다는 데 착안하여

을 생각하고, 좌변의 분자를 전개하여 로 나눈 다음 으로 놓고 에 관한 방정식을 풀어서 극점의 좌표를 구하였다. 이것은 오늘날의

에서 x를  구하는 것에 해당하는 것이다.

  뉴턴은 1704년에 출판된 ≪광학≫의 부록 '곡선의 구적에 대하여'에서 다음과 같이 말하고 있다.

  "수학적 양이 대단히 작은 부분으로 이루어진 것이 아니고 연속적인 운동에 의하여 그려진 것으로 생각한다. 선은 그 작은 부분을 연결해서 생긴 것이 아니고 점의 연속적인 운동에 의하여 이루어졌으며, 면은 선의 운동으로 이루어지고, 입체는 면의 운동으로 이루어진다고 생각한다. 각은 그 변의 회전에 의하여 이루어지고, 시간은 연속적인 흐름에 의하여 생긴다."

  뉴턴은 운동에 관한 문제를 설명하기 위하여 속도, 가속도의 개념을 수학적으로 정식화하여 유율의 개념을 도입하였다.

  즉, 흐르는 양을 유량(fluent)이라 하고, 흐르는 양을 독립변수(여기서는 시간)의 함수로 보면서, 유량의 변화량을 흐름의 속도로 생각하며 이것을 유율(fluxion)이라고 하였다.

  뉴턴은 유량을  x,y 등으로 나타내고, 유율을, x, y등으로 나타내었으며, 유율을 계산하기 위하여 무한히 작은 변화를 생각하여 이를 모멘트(moment)라고 하였다. 모멘트는 오늘날의 변수와 함수의 증분을 뜻하는 것이다. 그리하여 유율의 계산을 위에서 말한 페르마의 방법과 거의 같은 방법으로 하였다.

  라이프니츠는 곡선에 접선을 긋는 문제와 직선군이 주어졌을 때, 이들 모든 직선을 접선으로 가지는 곡선(오늘날의 포락선)을 구하는 문제와의 관계를 조사하였다. 그리고 접선을 구하는 문제와 곡선을 구하는 문제는 서로 역연산의 관계가 있다는 사실에 착안하여 미분법과 적분법 사이의 관계를 찾아내고, 미분방정식의 해법의 기초를 마련하였다.

  라이프니츠는 뉴턴과는 달리 기하학적, 대수적인 이론으로 미분법과 적분법을  설명하였다. 즉, 라이프니츠의 미분법은 기하적인 접선을 매개로 하여 정의되었으며, 구적법은 역접선의 방법의 특수한 경우임을 보여 미분방적식의 해법을 소개한 것이다.

  라이프니츠의 큰 공헌 중의 하나는 미분법과 적분법의 기호를 고안한 것이다. 뉴턴은 미분 기호 x를 사용하였으나, 라이프니츠는 dx를 사용하였고 dF(x)=F(x)dx에서  가 된다는 적분 기호도 라이프니츠가 고안한 것이다.

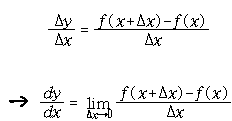
를 구하는 정식화된 기호는 코시에 의하여 만들어졌다.

 17세기 수학의 특징

유럽은 17세기에 접어들면서 철학, 천문학, 물리학 등의 발전과 더불어 근대, 그리고 현대에 이어지는 이른바 '과학혁명의 시대'에 돌입하게 된다.

이 세기에는 과학혁명기다운 눈부신 발견과 창의가 차례로 쏟아져 나왔다. 케플러, 네이피어, 페르마를 비록하여 데카르트, 파스칼, 뉴턴, 라이프니츠 등이 새로운 분야를 개척하였다.

이 들은 예외없이 물리학·천문학·철학 등의 여러 분야까지 점하여 연구한 천재들이였으며, 이런 면에서 후대의 수학자들과는 다시 그 면목을 달리하고 있다. 그들의 연구나 창의적 발견에도 이 특색이 잘 나타나 있다. <방법론서설>을 지은 철학자 데카르트는 해석기하학의 창시자로서 불후의 이름을 남기고있다. 기하학을 대수학과 결부시켜서 대수학적 방법을 발견하였다. 이것은 라이프니츠의 미적분 발견에 영향을 끼치고 있다고 보고 있다.

뉴턴과 라이프니츠는 각각 독립적으로 미적분학을 창시하여 근대해석학의 발단을 열었다. 수백년 동안 진전이 없었던 수학이 급속히 진보하여 기하학·대수학의 세계에서 해석학으로 비약하여 물리학에도 큰 영향을 끼쳤다.

뉴턴은 1671년에 미적분학을 체계화하였다. 우주의 중력의 법칙의 발견, 빛의 입자설등 찬란한 업적을 남겼다. <프린키피아, Philosophiae naturalis Principia mathematica>는 1687년에 간행되었다.

후에 라이프니츠와 뉴턴은 미적분학의 창설을 둘러싸고 많은 논쟁이 있었으나, 결국 양자는 각각 독립으로 그 업적을 이루었다는 것이 해명되었다. 라이프니츠는 수학의 기호화에도 큰 공적을 남겼다. 현재의 미적분학의 기호는 그에 힘입은 바가 크다. 법률학, 철학에도 큰 업적을 남겼다.